If Eph is the induced e.m.f. per phase in the alternator, there are following voltage drops occur in an alternator.
i) The drop across armature resistance Ia Ra both Ia and Ra are per phase values.
ii) The drop across synchronous reactance Ia Xs, both Ia and Xs are per phase values.
After supplying these drops, the remaining voltage of Eph is available as the terminal voltage Vph.
Note : Now drop Ia Ra is always in phase with Ia due to a resistive drop while current Ia lags by 90o with respect to drop Ia Xs as it is a drop across purely inductive reactance.
Hence all these quantities can not be added or subtracted algebraically but must be added or subtracted vectorially considering their individual phases. But we can write a voltage equation in its phasor from as,
This is called voltage equation of an alternator.
From this equation, we can draw the phasor diagram for various load power factor conditions and establish the relationship between Eph and Vph, in terms of armature current i.e. load current and the power factor cos(Φ).
For drawing the phasor diagram consider all per phase values and remember following steps.
Steps to draw the phasor diagram :
1. Choose current as a reference phasor.
2. Now if load power factor is cosΦ it indicates that angle between Vph and Ia is Φ as Vph is the voltage available to the load.
So show the phasor Vph in such a way that angle between Vph and Ia is Φ. For lagging 'Φ', Ia should lag Vph and for leading 'Φ', Ia should lead Vph. For unity power factor load Φ is zero, so Vph and Ia are in phase.
3. Now the drop Ia Ra is a resistive drop and hence will always be in phase with Ia. So phasor Ia Ra direction will be always same as Ia, i.e. parallel to Ia. But as it is to be added to Vph, Ia Ra phasor must be drawn from the tip of the Vph phasor drawn.
4. The drop Ia Xs is drop across purely inductive reactance. In pure inductance, current lags voltage by 90o. So 'Ia Xs' phasor direction will be always such that Ia will lag Ia Xs phasor by 90o. But this phasor is to be drawn from the tip of the Ia Raphasor to complete phasor addition of Vph, Ia Ra and Ia Xs.
5. Joining the starting point to the terminating point, we get the phasor Eph.
Whatever may be the load power factor, Ia Ra is a resistive drop, will be in phase with Ia while Ia Xs is purely inductive drop and hence will be perpendicular to Ia in such a way that Ia will lag Ia Xs by 90o. This is shown in the Fig. 1.
 |
| Fig. 1 |
By using the above steps, the phasor diagrams for various load power factor conditions can be drawn.
1.1 Lagging Power Factor Load
The power factor of the load is cosΦ lagging so Ia lags Vph by angle Φ. By using steps discussed above, phasor diagram can be drawn as shown in the Fig. 2.
 |
| Fig. 2 Phasor diagram for leading p.f. load |
To derive the relationship between Eph and Vph, the perpendicular are drawn on the current phasor from points A and B. These intersect current phasor at points D and E respectively.
... (Eph)2 = (OD + DE)2 + (BE - BC)2
... (Eph)2 = (Vph cosΦ + Ia Ra)2 + (VphsinΦ - Ia Xs)2
It can be observed that the sign of the Ia Xs is negative as against its positive sign for lagging p.f. load. This is because Xs consists of Xar i.e. armature reaction reactance. Armature reaction is demagnetising for lagging while magnetising for leading power factor loads. So sign of Ia Xs is opposite for lagging and leading p.f. conditions.
1.3 Unity Power Factor Load
The power factor of the load is unity i.e. cosΦ = 1. So Φ = 0, which means Vph is in phase with Ia. So phasor diagram can be drawn as shown in the Fig. 3.
 |
| Fig. 3 Phasor diagram for unity p.f. load |
Consider ΔOBC, for which we can write,
(OC)2 = (OB)2 + (BC)2
... (Eph)2 = (OA + AB)2 + (BC)2
... (Eph)2 = (Vph + Ia Ra)2 + (Ia Xs)2
As cosΦ = 1, so sinΦ = 0 hence does not appear in the equation.
Note : The phasor diagrams can be drawn by considering voltage Vph as a reference phasor. But to derive the relationship, current phasor selected as a reference makes the derivation much more simplified. Hence current is selected as a reference phasor.
It is clear from the phasor diagram that Vph is less than Eph for lagging and unity p.f. conditions due to demagnetising and cross magnetising effects of armature reaction. While Vph is more than Eph for leading p.f. condition due to the magnetising effect of armature reaction.
Thus in general for any power factor condition,
(Eph)2 = ( Vph cos + Ia Ra)2 + (Vph sin Ia Xs)2
+ sign for lagging p.f. loads
- sign for leading p.f. loads
and Vph = per phase rated terminal voltage
Ia = per phase full load armature current


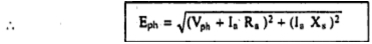
No comments:
Post a Comment