Consider a long, straight conductor with radius r meters and carrying a current I amperes as shown in the Fig.1(a).
 |
| Fig. 1 |
The magnetic field will be established due to this current. The magnetic flux lines will change inside the conductors which will contribute to induced voltage and hence inductance. The magnetic flux lines exist outside the conductor also. We may assume that the return path for the current in this conductor is far away and the magnetic field of the conductor is not affected. The value of inductance due to internal flux is given by the ratio of flux linkages to current by taking into account the fact that each line of internal flux links only a fraction of total current. The exact value of inductance of transmission line is obtained by considering the flux inside each conductor as well as external flux. The lines of flux are concentric with the conductor.
The mmf in ampere turns around any closed path is equal to the current in amperes enclosed by the path. Thus we have
where H is magnetic field intensity in At/m
Let the magnetic field intensity at a point x meters from the centre of the conductor be Hx. This is constant at all points as field is symmetrical. Thus integration of ds around the closed circular path is 2πx.
As Hx is constant
As the current density is uniform
Substituting this value of Ix in expression for Hx
If μ = μo μr, then flux density at the given point is given by,
μr = 1 for the non-magnetic material
For the element having thickness dx, the flux will be product of and the cross-sectional area of the element normal to the flux lines. This area is dx times axial length. If the axial length considered is 1m then the flux per meter of length is
This flux links with current Ix. Hence flux linkage per meter length of conductor is given by,
To find internal flux or the total flux linkage inside the conductor we have to carry the integration from the centre of conductor to its outside edge.
But μo = permeability of free space = 4π x 10-7 H/m
Thus we have obtained inductance per unit length of a round conductor due to flux inside the conductor. Inductance per unit length is referred as simply inductance for convenience and simplicity.




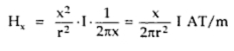






No comments:
Post a Comment